Question

If g(x) = x^2 + 6x with x ≥ -3, find g ^-1(0).

Please help and explain how to get the answer if you can.

Answer 1

Answer: 0

Explanation:

g(x) = x² + 6x ; x ≥ -3

To find the inverse, swap the x's and y's and solve for "y":

x = y² + 6y

x + 9 = y² + 6y + 9 add 9 to both sides to create a perfect square

x + 9 = (y + 3)²

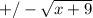`+/-√(x+9)` = y + 3 take square root of both sides

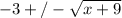`-3 +/-√(x+9)` = y ; y ≥ -3

g⁻¹(0) =
`-3 +/-√(0+9)`

=
`-3 +/-√(9)`

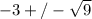
= -3 ± 3

= -3 + 3 , -3 - 3

= 0 , -6

since the restriction is: y ≥ -3, then -6 is not valid