Question

Median AM and CN of △ABC intersect at point O. What part of area of △ABC is the area of △AON?

Answer 1

The area of △AON
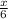`(x)/(6)` and the area of △ABC is x. The area of △AON is one-sixth part of △ABC.

Explanation:

Let the total area of △ABC be x.

A median of a triangle divides the area of a triangle in two equal parts.

Since AM are CN are medians, therefore the area of △ACN, △BCN, △ABM and △ATM are equal, i.e.,
`(x)/(2)`.

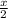A centroid is the intersection point of all medians of a triangle. A centroid divides each median in 2:1.

Since CN is median and O is the centroid of the triangle, therefore CO:ON is 2:1.

Draw a perpendicular on CN from A as shown in below figure. Let the height of the pendicular on CN from A be h.

`\frac{\text{Area of }\triangle ANO}{\text{Area of }\triangle ACN}=((1)/(2)* ON* h)/((1)/(2)* CN* h)=(1)/(3)`

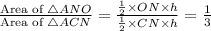
Therefore the area of △AON is one-third of △ACN.

`\text{Area of }\triangle ANO=(1)/(3)*\text{Area of }\triangle ACN`

`\text{Area of }\triangle ANO=(1)/(3)*(x)/(2)`

`\text{Area of }\triangle ANO=(x)/(6)`

`\frac{\text{Area of }\triangle ANO}{\text{Area of }\triangle ABC}=(((x)/(6)))/(x)=(1)/(6)`

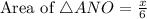
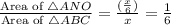
The area of ANO is
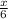`(x)/(6)`. Therefore the area of △AON is one-sixth part of △ABC.