Question

Seven-eighths of a sample of hydrogen-3 will have become a stable isotope after 36.9 years. What is the half-life of hydrogen-3?

Answer 1

A. 12.3 years

Step-by-step explanation:

Answer 2

12.3 years

Step by step Solution

Step 1

The first step is to use the radioactive decay formula to to calculate the radioactive constant for hydrogen 3. The radioactive formula is ,
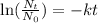`\ln(\tfrac{N_t}{N_0})=-kt` where
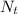`N_t` is the amount available at any time,
`N_0` is the initial amount of substance,
`k` is the radioactive decay constant. We are given the values
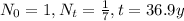`N_0=1,N_t=(1)/(7) , t=36.9y` . We use these values to calculate the constant as follows,

`\ln(\frac{\tfrac{1}{7}}{1})=-k(36.9)\\\\\implies k=-\frac{\ln(\tfrac{1}{8})}{36.9}=0.056y^(-1)`

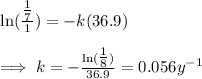
Step 2

The next step is to use the value for the decay constant to calculate the half life. We notice that at the half life, the value of the material remaining is 0.5. We show the calculation as shown below,

`t_{\tfrac{1}{2}}=(\ln(0.5))/(0.056)=12.3y`

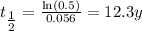
The half life is 12.3 years.