Answer: 1/6 part of the area of △ABC is the area of △AON
Explanation:
Here, ABC is a triangle.
In which, AM and AN are the median of the Δ ABC,
where,
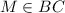 and
and
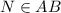 .
.
Since, By the property of the median,
Area of Δ ANC = Area of Δ BNC ( because median divide the triangle in two equal parts)
⇒ Area of Δ ANC = 1/2× Area of Δ ABC ------------ (1)
Now, Median AM and CN of △ABC intersect at point O. ( given)
That is, O is the centroid of the Δ ABC.
And, we know that, The centroid divides each median in a ratio of 2:1.
Thus, OC : ON = 2:1
Let OC = 2x and ON= x where x is any number.
Now, In triangle ANO,
Let h shows the height of Δ ANO,
Then the area of Δ ANO = 1/2 × x × h
And, area of Δ AOC = 1/2 × 2x × h ( because both triangles must have the same height)
But, the area of Δ AOC / area of Δ ANO = 2/1
⇒ AO divides the area of Δ ANC in the ratio of 2:1
That is, the area of Δ ANO = 1/3 × area of ANC
From equation (1) the area of Δ ANO = 1/3 × ( 1/2 × area of Δ ABC) = 1/6 × area of Δ ABC.
Thus, Area of Δ ANO is 1/6 th part of the area of Δ ABC.