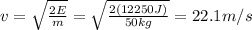Question

An object with mass of 50kg is dropping from a height of 25m. What is it’s velocity?

Answer 1

22.1 m/s

Step-by-step explanation:

We can solve the problem by using the conservation of energy. The mechanical energy is equal to the sum of kinetic energy and potential energy, and it is constant:

`E=K+U=(1)/(2)mv^2+mgh`

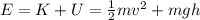
where

m is the mass

v is the velocity

g is the gravitational acceleration

h is the heigth of the object

At the moment when the object is dropped, the velocity is still zero, so K=0 and all the energy is gravitational potential energy:

`E=U=mgh=(50 kg)(9.8 m/s^2)(25 m)=12250 J`

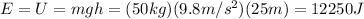
When the object reaches the ground, the height becomes zero: h=0, so the gravitational potential energy is zero and all the energy is now kinetic energy:

`E=K=(1)/(2)mv^2`

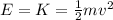
So, we can find the velocity:

`v=\sqrt{(2E)/(m)}=\sqrt{(2(12250 J))/(50 kg)}=22.1 m/s`