Question

asked Nov 25, 2019 86.4k views

2 Answers

Savoo · Answer 1 · 2019-11-27T02:40:01+0000

Answer:

4.05 miles approximately.

Explanation:

The problem is asking for the perimeter of the rectangular figure which is defines as

P=2(l+w)

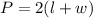
Where
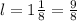l=1(1)/(8)=(9)/(8) and
w=(9)/(10)

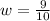
Replacing this values, we have

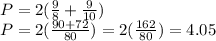
$P=2((9)/(8)+(9)/(10))\\P=2((90+72)/(80))=2((162)/(80))=4.05$

Therefore, the distance around the lot, the rectangular figure is 4.05 miles approximately.

Owlwalks · Answer 2 · 2019-12-02T14:39:54+0000

Answer:

The distance around the lot is 4.05 miles .

Explanation:

Formula

$Perimeter\ of\ rectangle = 2 (Length + Breadth)$

As given

$Helen’s\ house\ is\ located\ on\ a\ rectangular\ lot\ that\ is\ 1 (1)/(8)\ miles\ by\ (9)/(10)\ mile.$

i.e

$Helen’s\ house\ is\ located\ on\ a\ rectangular\ lot\ that\ is\ (9)/(8)\ miles\ by\ (9)/(10)\ mile.$

Here

$Length = (9)/(8)\ miles$

$Breadth = (9)/(10)\ miles$

Put in the formula

$Perimeter\ of\ rectangle = 2((9)/(8)+(9)/(10))$

L.C.M of (8,10) = 40

$Perimeter\ of\ rectangle = (2* (9* 5+9* 4))/(40)$

$Perimeter\ of\ rectangle = (2* (45+36))/(40)$

$Perimeter\ of\ rectangle = (2* 81)/(40)$

$Perimeter\ of\ rectangle = (81)/(20)$

Perimeter of rectangle = 4.05 miles

Therefore the distance around the lot is 4.05 miles .