Question

A bead of mass m = 5.0 kg is released from point A and slides on the frictionless track shown above. Note that the bead slides, it doesn't roll, because there's no friction at all.

(A) What is the total mechanical energy initially? - answer is 245 J

(B) Determine the bead's speed at point C? - answer is 7.67 m/s

I have no clue how to solve this pls help!! Picture is attached!

Answer 1

The total mechanical energy initially is 245 J, which is the potential energy at point A. The bead's speed at point C is 7.67 m/s.

Step-by-step explanation:

To solve this problem, we need to understand the concept of mechanical energy. Mechanical energy is the sum of an object's kinetic energy and potential energy. In this case, the bead is released from point A with no initial velocity, so its kinetic energy is zero. The potential energy at point A is given by the formula PE = mgh, where m is the mass of the bead, g is the acceleration due to gravity, and h is the height of point A above a reference point. Since the track is frictionless, the mechanical energy remains constant throughout the motion. The total mechanical energy initially is the potential energy at point A, which can be calculated as PE = mgh = (5.0 kg)(9.8 m/s^2)(5.0 m) = 245 J.

Now, to determine the bead's speed at point C, we can equate the initial potential energy at point A to the kinetic energy at point C. The kinetic energy is given by the formula KE = (1/2)mv^2, where m is the mass and v is the velocity. Since the bead slides, it does not roll, and there is no friction, the kinetic energy at point C is equal to the total mechanical energy initially. So, we have KE = 245 J = (1/2)(5.0 kg)v^2. Solving for v, we find v = sqrt((2*245 J)/(5.0 kg)) = 7.67 m/s.

Answer 2

The correct answer to the question is : (A) 245 J and (B) 7.92 m/s

EXPLANATION :

As per the question, the mass of the bead m = 5.0 Kg.

The height of the point A from the ground h = 5 m.

First we are asked to calculate the energy of the bead at point A.

The energy possessed by the bead at the point A is the gravitational potential energy.

Hence, the gravitational potential energy of the bead at the point A is calculated as -

Potential energy P.E = mgh

= 5 × 9.8 × 5 joule

= 245 J. [ANS]

Now we are asked to calculate the velocity at point C.

The potential energy of the bead at point B is equal to the kinetic energy of the bead at point C . It is so because the potential energy of the bead gradually converts into into kinetic energy when the bead comes from point B to point C.

Hence, potential energy at B = Kinetic energy at C.

⇒ mgh =
`(1)/(2)mv^2`

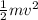
⇒ 2gh =
`v^2`

⇒ v =
`√(2gh)`

=
`√(2*9.8* 3.20)\ m/s`

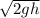
= 7.92 m/s. [ans]