Question

Which of the following options is an even function.

A. F(x)=sin(x+π)
B. F(x)=2sin(2x)
C. F(x)=cos(x+π)
D. F(x)=2sin(π+2π)

Answer 1

D) F(x) = 2sin(π+2π) = 2sin(3π) = 2 \cdot 0 = 0

==> F(x) = 2sin(π+2π) is an even function.

Correct answer: (D)

Answer 2

Option C -
`F(x)=\cos(x+\pi)`

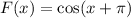
Explanation:

To find : Which of the following options is an even function?

Solution :

To determine the function is even,odd or neither we will find f(-x)

If f(-x) = - f(x) then function is odd.

If f(-x) = f(x) then function is even.

We know that,

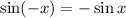`\sin(-x)=-\sin x` is always a odd function.

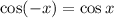`\cos(-x)=\cos x` is always an even function.

Now, In the following options

A.
`F(x)=\sin(x+\pi )`

`F(-x)=\sin(-(x+\pi))=-\sin (x+\pi)=-F(x)`

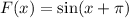
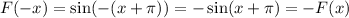
It is a odd function.

B.
`F(x)=2sin(2x)`

`F(-x)=2\sin(-2x)=-2\sin (2x)=-F(x)`

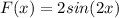
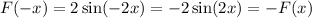
It is a odd function.

C.
`F(x)=\cos(x+\pi)`

`F(-x)=\cos(-(x+\pi))=\cos(x+\pi)=F(x)`

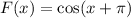
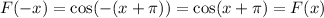
It is an even function.

D.
`F(x)=2\sin(\pi+\pi)`

`F(-x)=2\sin(-2x)=-2\sin (2x)=-F(x)`

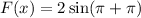
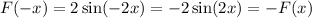
It is a odd function.

Therefore, Option C is correct.