Question

A supervisor records the repair cost for 22 randomly selected VCRs. A sample mean of $75.50 and standard deviation of $18.07 are subsequently computed. Determine the 99% confidence interval for the mean repair cost for the VCRs. Assume the population is approximately normal.

Answer 1

The 99% confidence interval for the mean repair cost for the VCRs

(65.801, 85.199)

Explanation:

Explanation:-

Mean of the sample(x⁻) = $75.50

Given the standard deviation of the sample (S) = $18.07

Given the size of the sample 'n' = 22

Degrees of freedom = n-1 =22-1 =21

critical value t₍₀.₀₁, ₂₁₎ = 2.5176

The 99% confidence interval for the mean repair cost for the VCRs

`(x^(-) - t_(0.01) (S.D)/(√(n) ) , x^(-) +t_(0.01) (S.D)/(√(n) ))`

`(75.50 - 2.5176 (18.07)/(√(22) ) , 75.50 +2.5176 (18.07)/(√(22) ))`

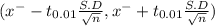
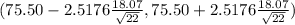
( 75.50 - 9.699 , 75.50 + 9.699 )

(65.801, 85.199)

Final answer:-

The 99% confidence interval for the mean repair cost for the VCRs

(65.801, 85.199)