Question

Verify that [tan(theta) + cot(theta)]^2 = sec^2(theta) + csc^2(theta)

Answer 1

(tanθ + cotθ)² = sec²θ + csc²θ

Expand left side: tan²θ + 2tanθcotθ + cot²θ

Evaluate middle term: 2tanθcotθ =
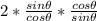`2*(sin\theta)/(cos\theta)*(cos\theta)/(sin\theta)` = 2

⇒ tan²θ + 2+ cot²θ

= tan²θ + 1 + 1 + cot²θ

Apply trig identity: tan²θ + 1 = sec²θ

⇒ sec²θ + 1 + cot²θ

Apply trig identity: 1 + cot²θ = csc²θ

⇒ sec²θ + csc²θ

Left side equals Right side so equation is verified