Question

Which table shows a proportional relationship between x and y?

A. x 3 6 8 10
y 12 15 18 20

B. x 1 2 7 8
y 0.5 1 3.5 4

C. x 3 7.5 15 20
y 1 2.5 4 6

D. x 2 3 4 5
y 7 9 11 13

Answer 1

Table B in doing the test right now so ill let you know if right or wrong

Explanation:

Answer 2

B

Explanation:

A proportional relationship is a relationship which crosses through the origin (0,0) and which has a proportional constant. We can determine this either by finding (0,0) where x=0 and y=0 in the table or by dividing y/x. None of the tables contain (0,0) so we will divide y by x. We are looking for a table which when each y is divided by its x we have the same constant appearing.

Table A

`(12)/(3) \\eq (15)/(6) \\eq (18)/(8) \\eq (20)/(10)`

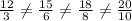
These fractions are not equal. This is not proportional.

Table B

`(0.5)/(1)=(1)/(2)  =(3.5)/(7) =(4)/(8)`

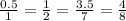
These fractions are equal and each shows the numerator to be half of the denominator. This is proportional.

Table C

`(1)/(3)\\eq (2.5)/(7.5) \\eq (4)/(15) \\eq (6)/(20)`

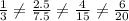
These fractions are not equal. This is not proportional.

Table D

`(7)/(2) \\eq (9)/(3)\\eq  (11)/(4) \\eq (13)/(5)`

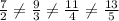
These fractions are not equal. This is not proportional.