Question

uincy uses the quadratic formula to solve for the values of x in a quadratic equation. He finds the solution, in simplest radical form, to be x = . Which best describes how many real number solutions the equation has?

Answer 1

Answer: according to spark notes: There can be 0, 1, or 2 solutions to a quadratic equation, depending on whether the expression inside the square root sign, (b2 - 4ac), is positive, negative, or zero. This expression has a special name: the discriminant.

In this case it is 0, not 2, which was my first and wrong answer

Answer 2

2 solutions

Explanation:

A quadratic equation has the formula:

`ax^(2) + bx +c = 0`

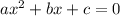
The solution of the equation is given as:

`x = \frac{-b+\sqrt{b^(2)-4ac } }{2a}`

The expression:
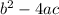`b^(2)-4ac` is known as the discriminant given by the symbol D.

Thus, the discriminant D, is given as D = b² - 4ac

There are several conditions to the solution.

If D < 0 the roots are imaginary. They are not real.

If D = 0, the solution has one real root

If D > 0, the solution as two distinct real roots (negative or positive)

A quadratic equation has only two real roots or solutions.