Question

Convert 3 - 3i to polar form.

a. ‘3sqrt(2)”cis” (pi)/4’

b. ‘3sqrt(2)”cis” (3pi)/4’

c. ‘3sqrt(2)”cis” (5pi)/4’

d. ‘3sqrt(2)”cis” (7pi)/4’

Answer 1

Option d is correct that is
`z=√(18) cos((7\pi)/(4))+i sin((7\pi)/(4))`

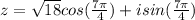
Explanation:

We have been given a complex number 3-3i we have to convert it in the polar form:

polar form of a complex number:

`z=r(cos{\theta}+i sin{\theta})`

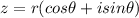
Where,
`r=√(x^2+y^2)`

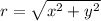
the general form of complex number is:

x+iy

Here, x=3 and y=-3

Hence,
`r=√(3^2+(-3)^2)=√(18)`

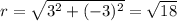
And
`\theta=tan^(-1)(y)/(x)`

`\theta=tan^(-1)(-3)/(3)`

`\Rightarrow \theta=tan^(-1)(-1)`

`\Rightarrow \theta=2{\pi}-(\pi)/(4)`

`\Rightarrow \theta=(7\pi)/(4)`

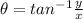
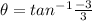
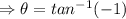
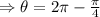
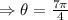
Hence, substituting all the values in polar form formula we get:

`z=√(18) cos((7\pi)/(4))+i sin((7\pi)/(4))`

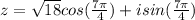
Therefore, option d is correct.