Question

Help!!!

A population of bacteria is growing exponentially according to the model

P=100e0.60t
Initially, there were 100 bacteria, but after how many hours will 400 colonies be present? How much time will it take (where P is the number of colonies and t is measured in hours. ) (Round to the nearest tenth).

Answer 1

Time it will take t = 23.1 (round to the nearest tenth)

Explanation:

Given: A population of bacteria is growing exponentially;

According to the model;

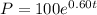`P = 100e^(0.60t)` ......[1]; where P is the number of colonies and t be the time measured in hours.

After how many hours will 400 colonies be present.

Substitute value of P = 400 in [1];

`400 = 100 e^(0.06t)`

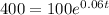
Divide both sides by 100 we get;

`4 = e^(0.06t)`

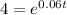
Taking ln both sides we get;

`ln 4 = ln e^(0.06t)`

Since;
`ln e^x = x`

then;

`ln 4 = 0.06 t`

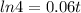
Divide both sides by 0.06 we get;

`t = (ln 4)/(0.06)`

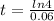
or

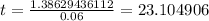`t =(1.38629436112)/(0.06) =23.104906` hours

Therefore, the time it will take is, t = 23.1 (round to the nearest tenth)