Question

Why is this the correct graph for the function

y= x^2 -16 / x+4 ???

Please explain !

Answer 1

The function
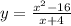`y=(x^(2)-16 )/(x+4)` simplifies to
`y=x-4` through factoring and division. Since
`y=x-4` is a linear function, this results in a line with y-intercept (0,-4) and slope 1.

Explanation:

The rational function
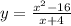`y=(x^(2)-16 )/(x+4)` can be simplified by factoring the numerator. The numerator is a difference of squares quadratic which factors as shown:

`y=((x+4)(x-4) )/(x+4)`

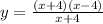
We can now divide (x+4) into the numerator which cancels out and leaves:

`y=x-4`

To graph a linear line, we find the y-intercept -4 on the y-axis and plot the point. From that point we rise 1 and run 1 for a slope of 1. We connect the two points.