Answer:
Function rule for the arithmetic sequence is;
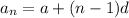
The 224th term of the arithmetic sequence is: 671
Explanation:
Arithmetic sequence: A sequence of number which increases or decreases by a constant amount each term.
Formula for nth term of arithmetic sequence is:
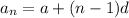
where a is the first term in the sequence, d is the common difference and n is the number of terms;
Given an arithmetic sequence:
2, 5 , 8, 11, ......
First term(a) = 2
Common difference(d) = 3 (Because the difference between the two consecutive terms is 3) i,e
5-2 = 3
8-5 = 3
11 -8 =3 ans so on,....
To find the 224th term;
we have,
a = 2 , d = 3 and n = 224
Using formula for nth arithmetic sequence;
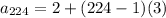
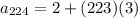
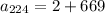 =671
=671
therefore, the 224th term for the given arithmetic sequence is, 671