Question

Sarah would like to make a 6 lb nut mixture that is 60% peanuts and 40% almonds. She has several pounds of a mixture that is 80% peanuts and 20% almonds and several pounds of a mixture that is 50% peanuts and 50% almonds.

a. What is the system that models this situation?
b. What is the solution to the system? How many pounds of the 80/20 mixture? How many pounds of the 50/50 mixture?

Answer 1

a. The system of equations that models the situation is....

`0.80x+0.50y=3.60\\\\ 0.20x+0.50y=2.40`

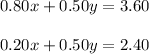
b. The solution to the system: x = 2 and y = 4

The amount of 80/20 mixture is 2 pounds and the amount of 50/50 mixture is 4 pounds.

Explanation:

Suppose, the amount of 80/20 mixture is
`x` pounds and the amount of 50/50 mixture is
`y` pounds.

So, the amount of peanuts in 80/20 mixture
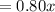`= 0.80x` pound and the amount of almonds in 80/20 mixture
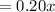`=0.20x` pound.

And the amount of peanuts in 50/50 mixture
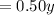`=0.50y` pound and the amount of almonds in 50/50 mixture
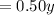`=0.50y` pound.

Now, Sarah would like to make a 6 pounds nut mixture that is 60% peanuts and 40% almonds.

So, the amount of peanuts in that mixture
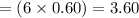`=(6* 0.60)=3.60` pounds

and the amount of almonds in that mixture
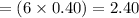`=(6 * 0.40)= 2.40` pounds.

So, the system of equations will be.........

`0.80x+0.50y=3.60 ...................(1)\\\\ 0.20x+0.50y=2.40...................(2)`

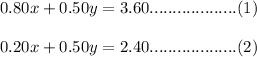
Subtracting equation (2) from equation (1), we will get.....

`(0.80x+0.50y)-(0.20x+0.50y)=3.60-2.40\\ \\ 0.60x=1.20\\ \\ x= (1.20)/(0.60)=2`

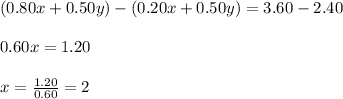
Now, plugging this
`x=2` into equation (1), we will get......

`0.80(2)+0.50y=3.60\\ \\ 1.60+0.50y=3.60\\ \\ 0.50y=3.60-1.60=2\\ \\ y=(2)/(0.50)=4`

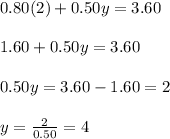
So, the amount of 80/20 mixture is 2 pounds and the amount of 50/50 mixture is 4 pounds.