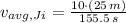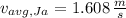Answer:
Jack:
Average velocity:
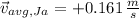 , Average speed:
, Average speed:
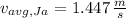
Jill:
Average velocity:
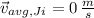 , Average speed:
, Average speed:
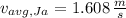
Step-by-step explanation:
We assume that each swimmer returns to the point of the departure each two lengths of the pool.
The average velocity is defined by the following definition:
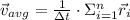 (1)
(1)
Where:
 - Total time, measured in seconds.
- Total time, measured in seconds.
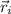 - i-th Relative vector position, measured in meters.
- i-th Relative vector position, measured in meters.
 - Number of lengths done by the swimmer.
- Number of lengths done by the swimmer.
And the average speed is represented by the following formula:
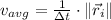 (2)
(2)
Where
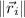 is the norm of the i-th relative vector position, measured in meters.
is the norm of the i-th relative vector position, measured in meters.
Now, we proceed to calculate both values for both swimmers:
Jack - Average velocity (
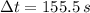 ,
,
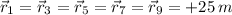 ,
,
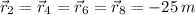 )
)

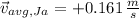
Jack - Average speed (
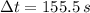 ,
,
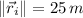 ,
,
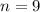 )
)
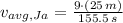
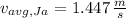
Jill - Average velocity (
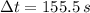 ,
,
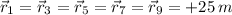 ,
,
 )
)
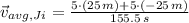
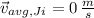
Jill - Average speed (
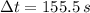 ,
,
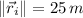 ,
,
 )
)