Question

a line segment has end points (-5, 7) and (4,-3) find the inverse of the line segment and graph both the segment and its inverse.

Answer 1

Answer

See graph

Explanation

The given line segment passes through the point
`(-5,7)` and
`(4,-3)`.

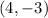
We plot this points and draw a straight line to them to obtain the blue line as shown in the

attachment.

The slope of this line segment is given by the formula


`m=(y_2-y_1)/(x_2-x_1)`

This implies that,


`m=(7--3)/(-5-4)`


`m=-(10)/(9)`

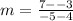
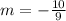
The equation of this line is given by the formula,


`y-y_1=m(x-x_1)`


`y+3=-(10)/(9)(x-4)`


`9y+27=-10(x-4)`


`9y+27=-10x+40`


`9y=-10x+13`

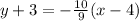
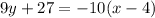
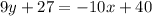
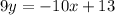
We now find the inverse by interchanging x and y.


`9x=-10y+13`

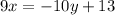
We now make y the subject,


`9x-13=-10y`


`y=-(9)/(10)x+(13)/(10)`

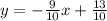
We now plot some points.

When


`x=7`


`y=-(9)/(10)* 7+(13)/(10)`


`y=-(50)/(10)=-5`

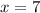
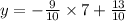
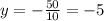
This gives the ordered pair


`(7,-5)`

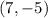
Also when


`x=-3`


`y=-(9)/(10)* -3+(13)/(10)`


`y=(40)/(10)=4`

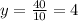
This gives the ordered pairs,


`(-3,4)`

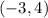
We plot these points too and draw a straight line through them to get the red line in the attachment.