Answer:
The solution can be defined as follows:
Explanation:
Augmented matrix for the given system is
![\left[\begin{array}{ccccc}2&1&-2&|&4\\4&0&2&|&10\\ -4&5&-17&|&-15 \end{array}\right]](https://img.qammunity.org/2022/formulas/mathematics/college/zh9bykmeuj4ltyauqwsnh0piz2j8llsdol.png)
Apply elementary row transformations on the matrix:
![R_1\to R_2 (2) \sim \left[\begin{array}{ccccc}4&2&-4&|&8\\4&0&2&|&10\\ -4&5&-17&|&-15 \end{array}\right] \\\\\\R_2\to R_2-R_1\\R_3\to R_3 (1)/(7) \sim \left[\begin{array}{ccccc}4&2&-4&|&8\\0&-1&3&|&1\\ 0&1&-3&|&-1 \end{array}\right] \\\\R_3\to R_3+R_2 \sim \left[\begin{array}{ccccc}4&2&-4&|&8\\0&-1&3&|&1\\ 0&0&0&|&0 \end{array}\right]](https://img.qammunity.org/2022/formulas/mathematics/college/ls2g2yiwlzm0kch8b85rvrrr8ew9tgpheh.png)
Matrix Ranking = 2 = Matrix Ranking So the method in question is consistent
And there are endless options. To be the equation,
We're having
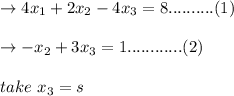
from equation 2 we get
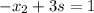
Substituting
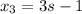 in equation 1 we get
in equation 1 we get
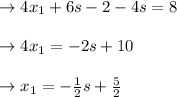
![\left[\begin{array}{c}X_1\\x_2\\x_3\end{array}\right]= \left[\begin{array}{c}-(1)/(2)s +(5)/(2) \\3s-1\\s\end{array}\right]](https://img.qammunity.org/2022/formulas/mathematics/college/u4fzfikeo4nyjyip9r8mciba1t43sx0td0.png)