Question

Which of the following functions is graphed below?

Answer 1

Answer: The correct option is (D)

`y=\begin{array}{cc}\{ &\begin{array}{cc}x^2-4 & x\leq 1\\x^2+3 & x>1\end{array}\end{array}`

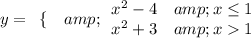
Step-by-step explanation: We are given to select the correct function that is graphed in the figure.

We have,

`\textup{If }y=x^2-4,\textup{ then }y(1)=1^2-4=1-4=-3,\\\\\textup{If }y=x^2+3,\textup{ then }y(1)=1^2+3=1+3=4.`

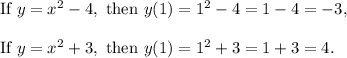
In the graph, there is closed hole at y = - 3, so y = - 3 (x = 1) is included.

Also, there is an open hole at y = 4, so y = 4 (x = 1) is excluded.

So, If y = x² - 4, then x will be greater than or equal to 1.

If y = x² + 3, then x will be less than 1.

Also,

`\textup{for }x\leq 1,~~y\leq x^2-4,\\\\\textup{for }x> 1,~~y> x^2+3.`

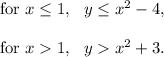
Therefore, the graphed function will be

`y=\begin{array}{cc}\{ &\begin{array}{cc}x^2-4 & x\leq 1\\x^2+3 & x>1\end{array}\end{array}`

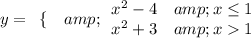
Option (D) is the correct function.