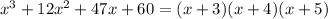Question

Write an expression that represents the width of a rectangle with length x+5 and area +^3+12^2+47x+60

Answer 1

x^2+7x+12

Step-by-step explanation:

For Algebra Nation:

Write an expression that represents the width of a rectangle with length x+5 and area x^3+12x^2+47x+60.

Answer 2

*** Correction in the question: Area =
`x^3+12x^2+47x+60` ***

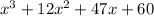The correct answer is: Width of rectangle (expression) = w =
`x^2+7x+12`

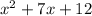
Step-by-step explanation:

The area of rectangle is given as follows:

Area.= Width * Length --- (A)

Where,

Area = A =
`x^3+12x^2+47x+60`

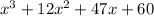
Length = l = x + 5

Width = w = ?

Plug in the values in equation (A) and solve for Width (w), as follows:

A = l * w

`x^3+12x^2+47x+60 = (x+5) * w \\ By\thinspace using\thinspace synthetic \thinspace division \thinspace you\thinspace will\thinspace get \thinspace the\thinspace following:\\(x+3)(x+4)(x+5) = (x+5) * w \\ w = (x+3)(x+4) \\ w = x^2+7x+12`

Therefore, the answer is: width =
`x^2+7x+12`

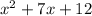
EXTRA NOTE: I have done synthetic division directly above, but let me explain how I did that.

First you need to guess the value that will yeild the value 0 when you plug in that value in the following equation:

`x^3+12x^2+47x+60`

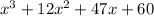
As you can see in the above-mentioned expression that every sign is positive; therefore, the value must be negative so that the values can be cancelled out and give us the result 0.

Let us try the value -1 first:

`(-1)^3+12(-1)^2+47(-1)+60 \\ -1+12-47+60\\24\\eq 0`

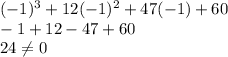
Let us try the value -2:

`(-2)^3+12(-2)^2+47(-2)+60 \\ -8+48-94+60\\6\\eq 0`

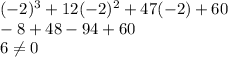
Let us try the value -3:

`(-3)^3+12(-3)^2+47(-3)+60 \\ -27+108-141+60\\0=0`

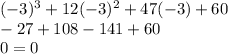
Hence, the one root is x = -3.

Now apply the synthetic division.

-3 |1 12 47 60

-3 -27 -60

---------------------

1 9 20 0

The expression will now become the following:

`1x^2+9x+20 \\ x^2 + 4x + 5x + 20 \\ x(x+4)+5(x+4) \\ (x+4)(x+5)`

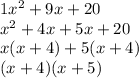
And the other one was (x+3) since x = -3 was one root.

Hence
`x^3+12x^2+47x+60 = (x+3)(x+4)(x+5)`