Answer:
- m∠1=m∠4=m∠5=m∠8=67°;
- m∠2=m∠3=m∠6=m∠7=113°.
Explanation:
Consider two parallel lines a and b with transversal m. These lines form 8 angles.
Note that
Since the difference of two angles is 46°, then these angles should be, for example, ∠1 and ∠2. These angles are supplementary, then
m∠1+m∠2=180°.
Solve the system of two equations:
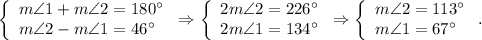
Then
- m∠1=m∠4=m∠5=m∠8=67°;
- m∠2=m∠3=m∠6=m∠7=113°.