Answer:
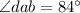
Explanation:
Given: It is given that a quadrilateral abcd is given in which ab is parallel to dc and the measure of ∠d is 96 degrees.
To find: The measure of the ∠DAB.
Solution: It is given that a quadrilateral abcd is given in which ab is parallel to dc and the measure of ∠d is 96 degrees.
Now, using the corresponding angle property in quadrilateral abcd, we have
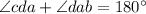
Substituting the given values, we get

⇒
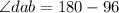
⇒
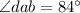
Thus, the measure of
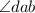 is
is
 .
.