Question

A(5 1) b(1 5) and c(-3 -1) are the vertices of triangle abc. find the LENGTH of median ad

Answer 1

`\text{Length of median AD}=√(37)`

Explanation:

We are given the vertices of triangle ABC. We need to find the length of median AD.

Please see the attachment for figure.

D is mid point of BC because median bisect the opposite side of triangle.

Using the formula of mid point. we get coodrinate of D

`\text{Mid Point :}\left ( (x_1+x_2)/(2),(y_1+y_2)/(2) \right )`

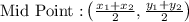
D is mid point of B(1,5) and C(-3,-1)

`\therefore D \left ( (1-3)/(2),(5-1)/(2) \right )\Rightarrow (-1,2)`

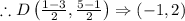
AD is median of triangle ABC. Now we find length of median AD using distance formula of two coordinate.

`\text{Distance }=√((x_2-x_1)^2+(y_2-y_1)^2)`

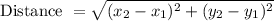
A(5,1) and D(-1,2)

`AD=√((5+1)^2+(1-2)^2)\Rightarrow √(36+1)`

`\text{Length of median AD}=√(37)`

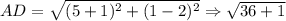
Thus,
`\text{Length of median AD}=√(37)`