Question

The measures of two consecutive angles of a parallelogram are in the ratio 6:3. What is the measure of an acute angle of the parallelogram?

Answer 1

60 degrees

Explanation:

Answer 2

The measure of an acute angle of the parallelogram is
`60^(\circ)`.

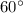Explanation:

As we know by the property of parallelogram :

Consecutive angles of a parallelogram are supplementary.

Given: The measure of two consecutive angles of a parallelogram are in the ratio 6: 3.

Then;

6x be the measure of larger angle and 3x be the measure of smaller angle.

⇒
`6x + 3x =180^(\circ)`

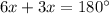
Combine like terms;

`9x =180^(\circ)`

Divide both sides by 9 we get;

`(9x)/(9) =(180)/(9)`

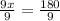
Simplify:

`x = 20^(\circ)`

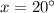
Then, the measure of larger angle 6x =
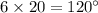`6 * 20 = 120^(\circ)` and

the measure of smaller angle 3x =
`3 * 20^(\circ)=60^(\circ)`.

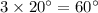Since, we know that in a parallelogram, opposite interior angles are equal.

Acute angle is an angle smaller than a right angle(i.e 90 degree)

Therefore, the measure of an acute angle of the parallelogram is
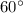`60^(\circ)`.