Question

Carla looks from a height of 14 yards at the top of her apartment building. She lines up the top of the flagpole with the curb of a street 20 yards away. If the flagpole is 12 yards from the apartment building, how tall is the flagpole to the nearest tenth

Answer 1

5.6 yards.

Step-by-step explanation:

Please find the attachment.

Let x be the height of flagpole.

We have been given that Carla looks from a height of 14 yards at the top of her apartment building. She lines up the top of the flagpole with the curb of a street 20 yards away.

We can see from our attachment that the flagpole and apartment are forming two right triangles, so we will use proportions to solve for height of the given flagpole.

The height of flagpole corresponds to height of the apartment.

`(14)/(x)=(20)/(8)`

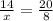
Upon cross multiplying our equation we will get,

`20x=14* 8`

`20x=112`

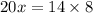
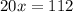
Dividing both sides of our equation by 20 we will get,

`(20x)/(20)=(112)/(20)`

`x=(112)/(20)`

`x=5.6`

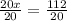
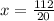
Therefore, the height of the flagpole is 5.6 yards.