Question

Ben claims that the points (2 4) (4 8) and (8 12) lie on a line. show that ben is incorrect

Answer 1

Ben is incorrect because the slopes of the lines between two points are not same.

Explanation:

The given points are (2,4), (4,8) and (8,12).

If all the points lie on a straight line, then the slopes of the line joining the pair of points are same.

Slope formula is

`m=(y_2-y_1)/(x_2-x_1)`

The slope of line joining (2,4) and (4,8).

`m_1=(8-4)/(4-2)`

`m_1=(4)/(2)`

`m_1=2`

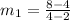
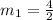
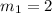
The slope of line joining (2,4) and (8,12).

`m_2=(12-4)/(8-2)`

`m_2=(8)/(6)`

`m_2=(4)/(3)`

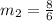
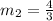
The slope of line joining (4,8) and (8,12).

`m_3=(12-8)/(8-4)`

`m_3=(4)/(4)`

`m_3=1`

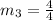
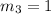
Since the slopes are not equal therefore these points lies on different lines.

Hence proved that ben is incorrect.