Answer:
The dimension of box=

Explanation:
We are given that
Volume of box=4 cubic feet
Let x be the side of square base and h be the height of box
Volume of box=



Now, surface area of box,A=







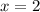

Substitute x=2

Hence, the area of box is minimum at x=2
Therefore, side of square base,x=2 ft
Height of box,h=

Hence, the dimension of box=
