Answer: The probability that the 7th chip is red = 0.4
Explanation:
Given that;
an urn contains 40 red chips and 60 white chips
6 chips are randomly drawn and discarded and a 7th chip is drawn,
lets consider E as the the event that represent the 7th chip is red.
so probability that 7th chip is red will be;
P(E) = ⁶∑
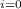
![\left[\begin{array}{ccc}40\\i\\\end{array}\right]](https://img.qammunity.org/2022/formulas/mathematics/college/2tiu0ob9ir28aley0g0bat0gvt66jkjmxp.png)
![\left[\begin{array}{ccc}40\\6-i\\\end{array}\right]](https://img.qammunity.org/2022/formulas/mathematics/college/vc7ob20r9qhe1ckrbuygo8uw88pg3bwqs0.png) ×
×
![\left[\begin{array}{ccc}40-i\\1\\\end{array}\right]](https://img.qammunity.org/2022/formulas/mathematics/college/ol971agh0mgfoc9uha6g8defpxvcqfus0d.png) /
/
![\left[\begin{array}{ccc}100\\6\\\end{array}\right]](https://img.qammunity.org/2022/formulas/mathematics/college/aywotzxcfowvfjtum4gifa4b3aw3vurmp6.png)
![\left[\begin{array}{ccc}94\\1\\\end{array}\right]](https://img.qammunity.org/2022/formulas/mathematics/college/8m51oo1ecrj1e92dbwmec38rnqt2pgk3n5.png)
=
![\left[\begin{array}{ccc}40\\0\\\end{array}\right]](https://img.qammunity.org/2022/formulas/mathematics/college/rktupwwcdx845zsi1lzo80zdrp2ktd2iut.png)
![\left[\begin{array}{ccc}60\\6\\\end{array}\right]](https://img.qammunity.org/2022/formulas/mathematics/college/m8ef9otqppj77j9wjre0osyu9bc9lh26d3.png) ×
×
![\left[\begin{array}{ccc}40\\1\\\end{array}\right]](https://img.qammunity.org/2022/formulas/mathematics/college/b7rpwjvxvi1liklxi9bjr8aiv0o1o6fx6d.png) +
+
![\left[\begin{array}{ccc}40\\1\\\end{array}\right]](https://img.qammunity.org/2022/formulas/mathematics/college/b7rpwjvxvi1liklxi9bjr8aiv0o1o6fx6d.png)
![\left[\begin{array}{ccc}60\\5\\\end{array}\right]](https://img.qammunity.org/2022/formulas/mathematics/college/x8tcukiplxir9jboeylqchmbwkot6bxspt.png) ×
×
![\left[\begin{array}{ccc}39\\1\\\end{array}\right]](https://img.qammunity.org/2022/formulas/mathematics/college/553rkk64k49imdnbfe08mrd6l6j8jkpz0m.png) + ......+
+ ......+
![\left[\begin{array}{ccc}4\\6\\\end{array}\right]](https://img.qammunity.org/2022/formulas/mathematics/college/a9w2bli2wpo5et0s32jz3s93enw5rarjit.png)
![\left[\begin{array}{ccc}60\\0\\\end{array}\right]](https://img.qammunity.org/2022/formulas/mathematics/college/dchoykvavmqoqqzv5ok4ygalzdp5q8nw43.png)
![\left[\begin{array}{ccc}34\\1\\\end{array}\right]](https://img.qammunity.org/2022/formulas/mathematics/college/utkw9hbguwvi33dr1u779xk3kiqihai16m.png) /
/
![\left[\begin{array}{ccc}100\\6\\\end{array}\right]](https://img.qammunity.org/2022/formulas/mathematics/college/aywotzxcfowvfjtum4gifa4b3aw3vurmp6.png)
![\left[\begin{array}{ccc}94\\1\\\end{array}\right]](https://img.qammunity.org/2022/formulas/mathematics/college/8m51oo1ecrj1e92dbwmec38rnqt2pgk3n5.png)
= [ 2002554400 + ..... + 130504920 ] /
![\left[\begin{array}{ccc}100\\6\\\end{array}\right]](https://img.qammunity.org/2022/formulas/mathematics/college/aywotzxcfowvfjtum4gifa4b3aw3vurmp6.png)
![\left[\begin{array}{ccc}94\\1\\\end{array}\right]](https://img.qammunity.org/2022/formulas/mathematics/college/8m51oo1ecrj1e92dbwmec38rnqt2pgk3n5.png)
= 44821170240 / (1192052400)(94)
= 44821170240 / 112052925600
= 0.4
Therefore the probability that the 7th chip is red = 0.4