Question

A building contractor is to dig a foundation 50 feet long, 20 feet wide and 10 feet deep. The contractor pays $15 per load for trucks to remove the dirt. Each truckload holds 5 cubic yards of dirt. What is the cost to have all the dirt hauled away?

Answer 1

$1111.11

Explanation:

We have been given that a building contractor is to dig a foundation 50 feet long, 20 feet wide and 10 feet deep.

Let us find the volume of the dirt dig from the foundation.

`\text{Volume of dirt dig from foundation}=50\text{ feet}*20\text{ feet}*10\text{ feet}`

`\text{Volume of dirt dig from foundation}=10000\text{ feet}^(3)`

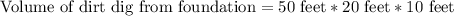
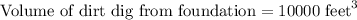
Since, 1 cubic feet= 0.037037 cubic yards. Let us convert volume of dirt dig into cubic yards by multiplying 10,000 by 0.037037.

`\text{Volume of dirt dig from foundation}=10000*0.037037=370.3704`

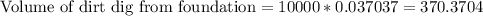
Now let us find how many truckload will hold 370.3704 cubic yards of dirt by dividing 370.3704 by 5.

`\text{Number of truckloads needed}=(370.3704 )/(5)`

`\text{Number of truckloads needed}=74.07408`

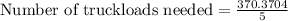
Now let us multiply number of truckloads by 15 to find the total cost to haul away all the dirt.

`\text{Total cost}=74.07408*15`

`\text{Total cost}=1111.1112`

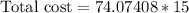
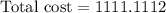
Therefore, the cost to have all the dirt hauled away is $1111.11.