Question

At zippy rent-a-car, you can rent a car for $25 per day,with a one-time fee of $100. At Speedy Rent-a-car you can rent a car for $30 per day with a one-time fee $30. Write and solve a system of equations to find the number of days for which both car rental locations will cost the same

Answer 1

Answer: day 14, 450

Explanation:

First one

125, 150, 175, 200, 225, 250, 275, 300, 325, 350, 375, 400, 425, 450, 475, 500

second one

60, 90, 120, 150, 180, 210, 240, 270, 300, 330, 360, 390, 420, 450

Answer 2

Answer: Required system of equations :

`y_1(x)= 100+25x`

`y_2(x)= 30+30x`

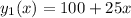
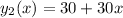
The number of days for which both car rental locations will cost the same = 14

Explanation:

Let x be the number of days .

Formula used here :

Total cost = One -time fee+ ( cost of renting car per day ) x (No. of days)

Given : At zippy rent-a-car, you can rent a car for $25 per day,with a one-time fee of $100.

i.e. One -time fee= $100

Cost of renting car per day =$25

Then, the total cost at zippy :
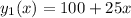`y_1(x)= 100+25x` (1)

At Speedy Rent-a-car you can rent a car for $30 per day with a one-time fee $30.

i.e. One -time fee= $30

Cost of renting car per day =$30

Then, the total cost at Speedy :
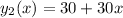`y_2(x)= 30+30x` (2)

According to the question , it
`y_1(x)=y_2(x)`

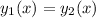
Then,
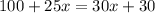`100+25x= 30x+30` (From (1) and (2))

`100-30= 30x-25x` [Subtract 30 and 25 x form both sides]

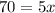`70= 5x` (Simplify)

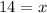`14=x` (Divide both sides by 5)

i.e. x= 14

Hence, the number of days for which both car rental locations will cost the same = 14