Answer:
The dimensions of the box of maximum volume are: Length: 6.325 centimeters, height: 3.162 centimeters.
Explanation:
The volume (
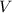 ), measured in cubic centimeters, and the surface area of the rectangular box (
), measured in cubic centimeters, and the surface area of the rectangular box (
 ), measured in square centimeters, with a square base are represented by the following formulas:
), measured in square centimeters, with a square base are represented by the following formulas:
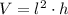 (1)
(1)
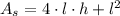 (2)
(2)
Where:
 - Length of the side of the square base, measured in centimeters.
- Length of the side of the square base, measured in centimeters.
 - Height of the box, measured in centimeters.
- Height of the box, measured in centimeters.
By (2) we clear the height:
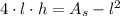
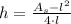
And expand (1) by this result:
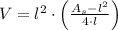
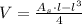
Lastly, we proceed to perform First and Second Derivative Test to find critical values associated with maximum volume:
First Derivative Test

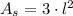
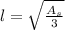 (1)
(1)
Second Derivative Test
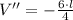

 (2)
(2)
We conclude that critical value leads to a maximum volume.
If we know that
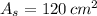 , then dimensions of the box are, respectively:
, then dimensions of the box are, respectively:



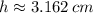
The dimensions of the box of maximum volume are: Length: 6.325 centimeters, height: 3.162 centimeters.