Question

Ammonia reacts with hypobromite OBr- as follows: NH3 OBr- ---> N2 Br- H20 which is the limiting reactant if 5.00 ml of 0.623 M NaOBr solution are added to

Answer 1

Limiting reactant: NaOBr or OBr⁻.

Left over: 0.0006317 moles of ammonia remain unreacted.

Step-by-step explanation:

Hello!

In this case, for the balanced chemical reaction:

`2NH_3 +3OBr^- \rightarrow N_2+ 3Br^- 3H_2O`

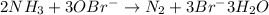
Thus, when 5.00 ml of 0.623 M NaOBr react with 183 μL of 14.8 M NH3, in order to identify the limiting reactant, we first compute the moles of each reactant:

`n_(OBr^-)=5.00mL*(1L)/(1000mL)*0.623(molNaOBr)/(L)*(1molOBr^-)/(1molNaOBr)=0.003115mol OBr^-\\\\n_(NH_3)=183\mu L*(1L)/(1x10^6\mu L) *14.8(molNH_3)/(1L) =0.0027084molNH_3`

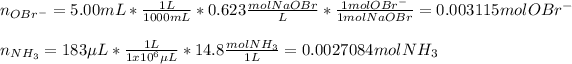
Now, we can compute the moles of any product, say nitrogen gas, produced by each reactant:

`n_(N_2)^(by\ NH_3) =0.0027084molNH_3*(1molN_2)/(2molNH_3) =0.0013542molN_2\\\\ n_(N_2)^(by\ OBr^-) =0.003115molOBr^-*(1molN_2)/(3molOBr^-) = 0.0010383molN_2`

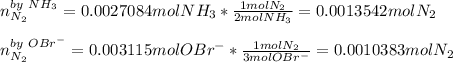
Therefore, since the hypobromite yields the fewest moles of nitrogen, we infer it is the limiting reactant. Moreover, for the left over of ammonia, we compute the required moles to yield 0.0010383 moles of nitrogen:

`n_(NH_3)^(required) =0.0010383molN_2*(2molNH_3)/(1molN_2) =0.002077molNH_3`

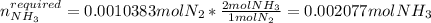
So the left over is:

`n_(NH_3)^(left\ over) = 0.0027084mol-0.0020767mol\\\\n_(NH_3)^(left\ over) =0.0006317molNH_3`

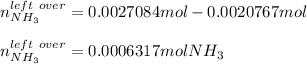
Best regards!