Question

Write the standard equation of a circle with center (−9, −4) and radius 5

Answer 1

A

Explanation:

the equation of a circle in standard form is

(x - h)² + (y - k)² = r²

where (h, k) are the coordinates of the centre and r is the radius

here (h, k) = (- 9, - 4) and r =
`√(5)` ⇒ r² = (
`√(5)`)² = 5

(x + 9)² + (x + 4)² = 5 → A

Answer 2

The right answer is A. :
`(x+9)^2+(x+4)^2=5`.

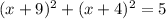Explanation:

The standard equation for a circumference with radius r, and center in the point with coordinates (h,k) is (x-h)^2+(x-k)^2=r^2.

Here, notice that for the statement of the problem we know that the radius is
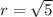`r=√(5)`. Then, r^2=5.

The coordinates of the center of the circumference is (-9,-4). Then the values of h and k are -9 and -4 respectively. Taking into account the rule of signs, (x-h)=(x+9) and (y-k)=(y+4).

Therefore, the standard equation of the circle is

(x+9)^2+(x+4)^2=5.