Question

Write the equation of the line perpendicular to 2x+3y=9 that passes through (-2,5). Write your answer in slope-intercept form. Show your work.

Answer 1

ANSWER


`y = (3)/(2) x + 8`



Step-by-step explanation

The line given to us has equation,


`2x + 3y = 9`

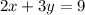
We need to write this equation in the slope intercept form to obtain,



`3y = - 2x + 9`




`\Rightarrow \: y = - (2)/(3)x + 3`


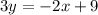
The slope of this line is


`m_1 = - (2)/(3)`
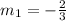
Let the slope of the perpendicular line be


`m_2`

Then

`m_1 * m_2 = - 1`



`- (2)/(3) m_2= - 1`

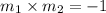
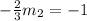
This implies that,


`m_2 = - 1 * - (3)/(2)`



`m_2 = (3)/(2)`



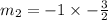
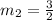
Let the equation of the perpendicular line be,


`y = mx + b`

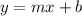
We substitute the slope to get,



`y = (3)/(2) x + b`

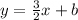
Since this line passes through

`(-2,5)`
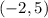
it must satisfy its equation.


This means that,


`5= (3)/(2) ( - 2)+ b`



`5 = - 3 + b`




`5 + 3 = b`



`b = 8`

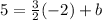
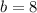
Wherefore the slope-intercept form is


`y = (3)/(2) x + 8`