Question

A spherical balloon with a 36cm diameter is being deflated. Its volume V is a function of its radius r according to

Answer 1

Question:

A spherical balloon with a 36 cm diameter is being deflated. Its volume V is a function of its radius r according to
`V(r) = (4)/(3)\pi r^3.`

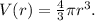
As it's deflating, it is much easier to measure its radius than its volume. Suppose the radius of the balloon is
`r(t) = 18 - 18e^(-0.24t)` cm at t seconds.

• Determine the value of V'(4) (accurate to 3 decimal places). Write a complete sentence including the units of both 4 and V'(4) in this context.

• Determine the value of r(4) (accurate to 3 decimal places). Write a complete sentence including the units of both 4 and r(4) in this context.

Answer:

`V'(4) = 201.143`

`r(4) = 11.106`

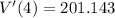
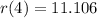
Step-by-step explanation:

Given

`V(r) = (4)/(3)\pi r^3.`

`r(t) = 18 - 18e^(-0.24)`

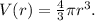
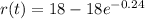
Solving (a): V'(4)

First, we determine V('r)

`V(r) = (4)/(3)\pi r^3.`

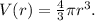
Differentiate w.r.t r

`V'(r) = 3 * (4)/(3)\pi r^(3-1)`

`V'(r) = 3 * (4)/(3)\pi r^2`

`V'(r) = 4\pi r^2`

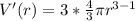
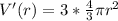
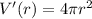
Substitute 4 for r and take
`\pi = (22)/(7)`

`V'(4) = 4 * (22)/(7) * 4^2`

`V'(4) = 4 * (22)/(7) * 16`

`V'(4) = (4 * 22* 16)/(7)`

`V'(4) = (1408)/(7)`

`V'(4) = 201.143`

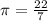
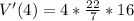
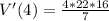
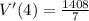
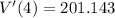
This means that the volume of the balloon when the radius is deflated to 4 seconds is 201.143 cm^3

Solving (b): r(4)

Substitute 4 for t in
`r(t) = 18 - 18e^(-0.24t)`

`r(4) = 18 - 18e^(-0.24*4)`

`r(4) = 18 - 18e^(-0.96)`

`r(4) = 18 - 18*0.383`

`r(4) = 11.106`

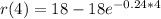
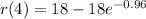
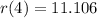
This means that the radius of the balloon when at 4 seconds of deflation is 11.106 cm