Question

Kite QRST has a short diagonal of QS and a long diagonal of RT. The diagonals intersect at point P. Side QR= 5 m and diagonal QS= 6m. Find the length of segment RP

Answer 1

`PR=4m`

Explanation:

Firstly, we will draw diagram for kite

we are given

QR=5m

QS=6m

we know that QPR is a right angled triangle

so, QP=PS

`QP=(1)/(2) QS`

`QP=(1)/(2)* 6`

`QP=3`

now, we can use Pythagoras theorem

`QR^2=QP^2+PR^2`

now, we can plug values

`5^2=3^2+PR^2`

`PR=4`

Answer 2

Given the statement: Kite QRST has a short diagonal of QS and a long diagonal of RT. The diagonals intersect at point P.

Properties of Kite:

• The diagonals are perpendicular

• Two disjoint pairs of consecutive sides are congruent by definition of kite

• One diagonal is the perpendicular bisector to the other diagonal.

It is given that: Side QR = 5m and diagonal QS = 6m.

Then, by properties of kite:

`QP = (1)/(2)QS`

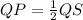
Substitute the value of QS we get QP;

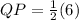`QP = (1)/(2)(6)` = 3 m

Now, in right angle
`\triangle RPQ`

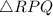
Using Pythagoras theorem:

`QR^2= RP^2 +QP^2`

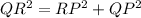
Substitute the given values we get;

`(5)^2= RP^2 +(3)^2`

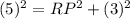
or

`25= RP^2 +9`

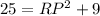
Subtract 9 from both sides we get;

`16= RP^2`

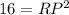
Simplify:

`RP = √(16) = 4 m`

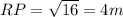
Therefore, the length of segment RP is, 4m