Question

in the figure below trianglePQM and triangleQRP are right triangles. the measure of lineQM is 6 and the measure of lineQP is 8. what is the measure of line PR?

Answer 1

Option 4 is correct. The length of PR is 6.4 units.

Explanation:

From the given figure it is noticed that the triangle PQR and triangle MQR.

Let the length of PR be x.

Pythagoras formula

`hypotenuse^2=base^2+perpendicular^2`

Use pythagoras formula for triangle PQM.

`PM^2=QM^2+PQ^2`

`PM^2=(6)^2+(8)^2`

`PM^2=36+64`

`PM^2=100`

`PM=10`

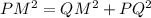
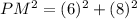
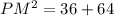
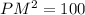
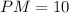
The value of PM is 10. The length of PR is x, so the length of MR is (10-x).

Use pythagoras formula for triangle PQR.

`PQ^2=QR^2+PR^2`

`(8)^2=QR^2+x^2`

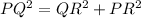
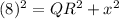
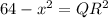`64-x^2=QR^2` .....(1)

Use pythagoras formula for triangle MQR.

`MQ^2=QR^2+MR^2`

`(6)^2=QR^2+(10-x)^2`

`36=QR^2+x^2-20x+100`

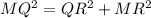
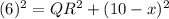
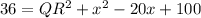
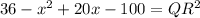`36-x^2+20x-100=QR^2` .... (2)

From equation (1) and (2) we get

`36-x^2+20x-100=64-x^2`

`20x-64=64`

`20x=128`

`x=6.4`

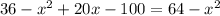
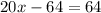
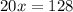
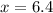
Therefore length of PR is 6.4 units and option 4 is correct.