Question

Suppose that rectangle ABCD is dilated to A'B'C'D' by a scale factor of 3 with a center of dilation at (1, 1).

What is the approximate distance from the center of dilation to the midpoint of C'D'?
A) 3 units
B) 4.5 units
C) 6.3 units
D) 9 units

Answer 1

Explanation:

The correct answer is c.

Answer 2

The correct option is C.

Explanation:

From the given figure it is noticed that the coordinates of vertices are C(1,-2) and D(-2,1).

Dilation by factor k with center at origin is defined as

`(x,y)\rightarrow(kx,ky)`

Dilation by factor k with center at point (a,b) is defined as

`(x,y)\rightarrow(k(x-a)+a,k(y-b)+b)`

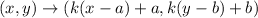
The scale factor is 3 and center of dilation at (1, 1).

`(x,y)\rightarrow(3(x-1)+1,3(y-1)+1)`

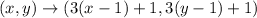
The coordinates of C' are

`(1,-2)\rightarrow(3(1-1)+1,3(-2-1)+1)\rightarrow(1,-8)`

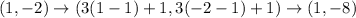
The coordinates of D' are

`(-2,1)\rightarrow(3(-2-1)+1,3(1-1)+1)\rightarrow(-8,1)`

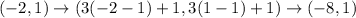
Midpoint of C'D is

`((-8+1)/(2), (1-8)/(2))=(-3.5,-3.5)`

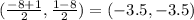
Distance formula is

`d=√((x_1-x_2)^2+(y_1-y_2)^2)`

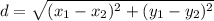
Distance between (-3.5,-3.5) and (1,1) is

`d=√((1+3.5)^2+(1+3.5)^2)`

`d=√((4.5)^2+(4.5)^2)`

`d=√(2(4.5)^2)`

`d=4.5√(2)`

`d=6.364`

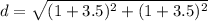
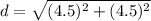
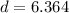
Therefore option C is correct.