ANSWER
D.
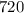
Step-by-step explanation
The infinite geometric series given to us is,
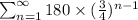
The first term of this series is,
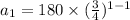
This implies that,
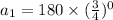
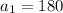
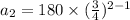
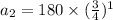
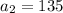
The common ratio of this sequence,
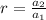
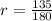
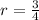
The sum to infinity of this series is given by the formula,
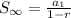
We substitute the above values to get,
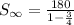
This simplifies to
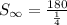
This implies that,
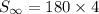
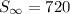
The correct answer is D.