Question

Maël mixes 1515 milliliters (\text{mL})(mL) of bleach with 3.753.75 liters (\text{L})(L) of water to make a sanitizing solution for a daycare. The amounts of bleach and water always have to be proportional when he makes sanitizing solution.

Which of the following could be combinations of volumes of bleach and water for Maël's sanitizing solution?
Choose 3 answers:
Choose 3 answers:

Answer 1

a b and c

Explanation:

Answer 2

Options A, B and C are correct choices.

Explanation:

We have been given that Mael 15 ml of bleach with 3.75 liters of water to make a sanitizing solution for a daycare.

Let us see our given options one by one to find which could be combinations of volumes of bleach and water for Mael's sanitizing solution.

Let us compare our given volume proportions with volume proportion of Mael's sanitizing solution.

A. 12 ml bleach and 3 liters of water.

`\frac{3.75\text{ Liters water}}{15\text{ ml bleach}}= \frac{3\text{ Liters water}}{12\text{ ml bleach}}`

`0.25\frac{\text{ Liters water}}{\text{ ml bleach}}=0.25\frac{\text{ Liters water}}{\text{ ml bleach}}`

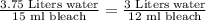
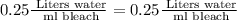
We can see that both proportions are equal, therefore, option A is a correct choice.

B. 6 ml bleach and 1.5 liters of water.

`\frac{3.75\text{ Liters water}}{15\text{ ml bleach}}= \frac{1.5\text{ Liters water}}{6\text{ ml bleach}}`

`0.25\frac{\text{ Liters water}}{\text{ ml bleach}}=0.25\frac{\text{ Liters water}}{\text{ ml bleach}}`

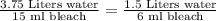
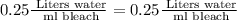
We can see that both proportions are equal, therefore, option B is a correct choice.

C. 3 ml bleach and 0.75 liters of water.

`\frac{3.75\text{ Liters water}}{15\text{ ml bleach}}= \frac{0.75\text{ Liters water}}{3\text{ ml bleach}}`

`0.25\frac{\text{ Liters water}}{\text{ ml bleach}}=0.25\frac{\text{ Liters water}}{\text{ ml bleach}}`

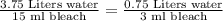
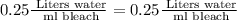
We can see that both proportions are equal, therefore, option C is a correct choice.

D. 20 ml bleach and 5.5 liters of water.

`\frac{3.75\text{ Liters water}}{15\text{ ml bleach}}= \frac{5.5\text{ Liters water}}{20\text{ ml bleach}}`

`0.25\frac{\text{ Liters water}}{\text{ ml bleach}}\\eq 0.275\frac{\text{ Liters water}}{\text{ ml bleach}}`

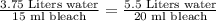
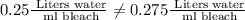
We can see that our both proportions are not equal, therefore, option D is not a correct choice.