Answer:
P(W) and P(B) are independent events.
Explanation:
Given : A bag contains 5 white marbles and 5 blue marbles. You randomly select one marble from the bag and put it back. Then, you randomly select another marble from the bag.
To find : Which calculation proves that randomly selecting a white marble the first time and a blue marble the second time are two independent events?
Solution :
Independent events - When the probability that one event occurs in no way affects the probability of the other event occurring.
We have given, 5 white marbles and 5 blue marbles.
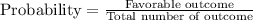
Total number of outcomes = 5+5=10
The probability that a white marble the first time,
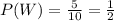
Their is a replacement occurs,
The probability that a blue marble the second time,
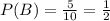
The probability of occurrence of a Blue marble is not affected by occurrence of the probability that we get white marble in first attempt.
Hence, P(W) and P(B) are independent events.