Question

One root of f(x)=x3-9x2+26x-24 is x=2. What are all the roots of the function? Use the remainder theorem.

Answer 1

2 , 3 and 4

Explanation:

Answer 2

All roots of the given function are, 2 , 3 and 4

Explanation:

Given the function f(x) =
`x^3-9x^2+26x-24`

Also, it given that x=2 is a root of the function f(x).

So, (x-2) is a factor of f(x).

Remainder theorem states that if a function is divided by (x-a), then the remainder is equal to f(a). If a function f(a) is equal to 0, therefore a is the root of the function.

We use synthetic method to divide f(x) by (x-2) as also shown in figure below;

`f(x) = (x-2)(x^2-7x+12)`

`f(x)=(x-2)(x^2-3x-4x-12)`

`f(x) = (x-2)(x(x-3)-4(x-3))`

`f(x) = (x-2)(x-3)(x-4)`

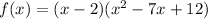
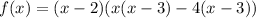
To find the roots of the function f(x) equate f(x) = 0.

we have;

`(x-2)(x-3)(x-4) =0`

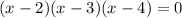
By zero product property states that if ab = 0, then either a = 0 or b = 0, or both a and b are 0.

x = 2 , 3 and 4.

Therefore, the roots of the given functions are; 2 , 3 and 4.