Question

The height of a trapezoid can be expressed as x – 4, while the bases can be expressed as x + 4 and x + 9. if the area of the trapezoid is 99 cm2 , find the length of the larger base.

Answer 1

Length of the larger base is 19 cm.

Explanation:

Height of the trapezoid = (x - 4)

Bases of the trapezoid = (x + 4) and (x + 9)

Area of the trapezoid = 99 cm²

We know the formula,

Area of trapezoid =
`(1)/(2)(\text{Sum of bases})* (\text{Distance between the bases}})`

99 =
`(1)/(2)[(x + 4)+(x + 9)](x - 4)`

99 =
`(1)/(2)[2x + 13](x - 4)`

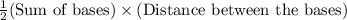
99×2 = (2x + 13)(x - 4)

198 = 2x² - 8x + 13x - 52

2x² + 5x - 52 - 198 = 0

2x² + 5x - 250 = 0

2x² + 25x - 20x - 250 = 0

x(2x + 25) - 10(2x + 25) = 0

(2x + 25)(x - 10) = 0

(2x + 25) = 0

2x = -25

x = -
`(25)/(2)`

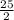
Since length of the base can not be negative.

Therefore, (x - 10) = 0 will be the solution

x = 10 cm

Length of the larger base = x + 9

= 10 + 9

= 19 cm

Answer 2

Answer: 19 cm

Explanation:

`A_(trapezoid)=(b_(1)+b_(2))/(2)*h`

99 =
`((x+4 + x+9)/(2)*(x - 4)`

99 =
`((2x + 13)/(2)*(x - 4)`

198 = (2x + 13)(x - 4)

198 = 2x² + 5x - 52

0 = 2x² + 5x - 250

0 = 2x²- 20x + 25x - 250

0 = 2x(x - 10) + 25( x - 10)

0 = (2x + 25)(x - 10)

0 = 2x + 25 or 0 = x - 10

`-(25)/(2)` = x or x = 10

Since length cannot be negative,
`-(25)/(2)` can be disregarded

Larger base: x + 9 = 10 + 9 = 19