We know that :
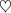 nth term of a Arithmetic Sequence is given by : a + (n - 1)d
nth term of a Arithmetic Sequence is given by : a + (n - 1)d
where : a is the first term
d is the common difference, which is given by difference between 2nd term and 1st term
Given Sequence : 15 , 23 , 31 , 39. . . . . .
We can notice that : a = 15
d = 2nd term - 1st term = (23 - 15) = 8
⇒ 61st term : 15 + (61 - 1)8
⇒ 15 + (60)8
⇒ 15 + 480
⇒ 495
⇒ 61st term of the given sequence is 495