Question

0.12 cubic meters of silver which she needs to make into 9.9e4 coins of thickness 2 mm. If she uses all of the silver, what is the diameter in centimeters of each coin

Answer 1

The diameter of each coin is approximately 2.778 centimeters.

Explanation:

According to the statement, 0.12 cubic meters (
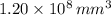`1.20* 10^(8)\,mm^(3)`) were used to produce 99000 coins. First, we calculate the volume of each coin (
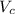`V_(c)`), measured in cubic meters, by dividing the total volume by the number of coins. That is:

`V_(c) = (1.20* 10^(8)\,mm^(3))/(99000)`

`V_(c) =1212.121\,mm^(3)`

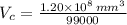
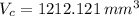
Then, diameter (
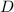`D`), measured in milimeters, can be derived from the following volume formula:

`V_(c) = (\pi)/(4)\cdot D^(2)\cdot h` (1)

Where
`h` is the thickness of the coin, measured in milimeters.

If we know that
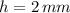`h = 2\,mm` and
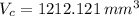`V_(c) =1212.121\,mm^(3)`, then the diameter of each coin is:

`D^(2) = (4\cdot V_(c))/(\pi\cdot h)`

`D = 2\cdot \sqrt{(V_(c))/(\pi\cdot h) }`

`D = 2\cdot\sqrt{(1212.121\,mm^(3))/(\pi\cdot (2\,mm)) }`

`D \approx 27.779\,mm`

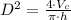
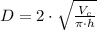
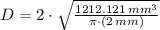
The diameter of each coin is approximately 2.778 centimeters.