Question

How do I solve this problem.

A person invested $8000 for 1 year, part at 4%, part at 11%, and the remainder at 13%. The total annual income from these investments was $882. The amount of money invested at 13% was $600 more than the invested at 4% and 11% combined. Find the amount invested at each rate.

Answer 1

The amounts invested at 4%, 11% and 13% are $1200, $2500 and $4300 respectively.

Explanation:

Let the amount invested at 4% be x and the amount invested at 11% be y.

Total amount of investment is $8000, so the amount invested at 13% is (8000-x-y).

The total annual income from these investments was $882.

`(4)/(100)* x+(11)/(100)* y +(13)/(100)* (8000-x-y)=882`

`(4x)/(100)+(11y)/(100)+(10400-13x-13y)/(100)=882`

`-9x-2y=-15800`

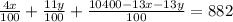
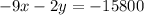
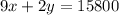`9x+2y=15800` ..... (1)

The amount of money invested at 13% was $600 more than the invested at 4% and 11% combined.

`8000-x-y=x+y+600`

`2x+2y=7400`

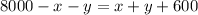
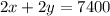
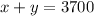`x+y=3700` ..... (2)

Solve equation (1) and (2) by using elimination method.

`x=1200`

`y=2500`

`8000-x-y=8000-1200-2500=4300`

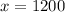
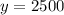
Therefore amounts invested at 4%, 11% and 13% are $1200, $2500 and $4300 respectively.