Question

“write an inequality to represent the graph.”

Answer 1

The inequality for the given graph is
`y>(2)/(3)x-1`.

Explanation:

From the given graph it noticed that the line passing through (0,-1) and (3,1).

The equation of line passing through two points is defined as

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

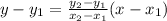
The equation of line is

`y+1=(1+1)/(3-0)(x-0)`

`y+1=(2)/(3)x`

`y=(2)/(3)x-1`

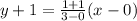
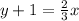
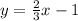
Therefore the related equation is
`y=(2)/(3)x-1`.

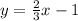The point (0,0) lies in the shaded region, therefore the point (0,0) is the solution of required inequality.

Put (0,0) in the related equation.

`0=(2)/(3)(0)-1`

`0=-1`

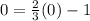
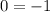
Since 0 is greater than -1, therefore the sign of inequality must be >. The related line is a dotted line, therefore we cannot use
`\geq`.

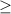Therefore the required inequality is

`y>(2)/(3)x-1`