Question

Of the shirts produced by a company, 6.5% have loose threads, 9.5% have crooked stitching, and 3% have loose threads and crooked stitching. Find the probability that a randomly selected shirt has loose threads or has crooked stitching.

Answer 1

`P(L\ or\ C) = 0.13`

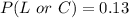
Explanation:

Given

Represent loose threads with L, Crooked stitching with C.

So, we have:

`P(L) = 6.5\%`

`P(C) = 9.5\%`

`P(L\ and\ C) = 3\%`

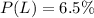
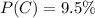
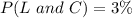
Required

Calculate P(L or C)

In probability:

`P(A\ or\ B) = P(A) + P(B) - P(A\ and\ B)`

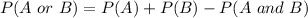
In this case:

`P(L\ or\ C) = P(L) + P(C) - P(L\ and\ C)`

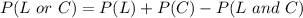
Substitute values for P(L), P(C) and P(L and C)

`P(L\ or\ C) = 6.5\% + 9.5\% - 3\%`

`P(L\ or\ C) = 13\%`

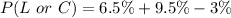
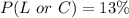
Convert to decimal

`P(L\ or\ C) = 0.13`

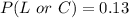
Hence:

The required probability is 0.13